Question

A line passes through the point (-6, 6) and (-6, 2). In two or more complete sentences, explain why it is not possible to write the equation of the given line in the traditional version of the point-slope form of a line. Type your answer in the box provided or use the upload option to submit your solution.

Answer 1

(-6,6)(-6,2)
notice how ur points have the same x coordinates....this means that u have a vertical line which has an undefined slope. Being that the slope is undefined, u cannot write the vertical line in slope intercept or point slope form.

Answer 2

The answer is undefined slope.

Explanation:

Firstly, we have to know about the traditional version of the point-slope form of a line.

The "point-slope" form of the equation of a straight line is:

`y-y_1=m*(x-x_1)`

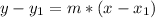
This equation is useful when we have:

1. one point on the line:
   `(x_1,y_1)`
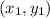
2. and the slope of the line:
   `m`

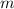
The slope can be determined with two points:

`m=(y_2-y_1)/(x_2-x_1)`

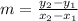
If we use the points:

`(x_1,y_1)=(-6,6)\\(x_2,y_2)=(-6,2)\\m=(2-6)/(-6+(-6))\\m=(-4)/(0)`

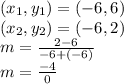
Then, we know that if there is a fraction with a zero denominator, the fraction is undefined, therefore the line is undefined too.

Finally, the answer is undefined slope.