Answer:
Pair of function Option B is Inverse of Each other.
Explanation:
A).
Given function: f(x) = 6x³ + 10
To find inverse first put y = f(x) then interchange y & x and solve for y
y = f(x)
x = f(y)
x = 6y³ + 10

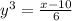
![y=^{\sqrt[3]{(x-10)/(6)}}](https://img.qammunity.org/2018/formulas/mathematics/high-school/1tgpvw2rv41vyq42teyddnmm9ervqvjepv.png)
By comparing with given inverse function.
Its clear its not the correct option.
B).
Given function: f(x) = 4x³ + 5
To find inverse first put y = f(x) then interchange y & x and solve for y
y = f(x)
x = f(y)
x = 4y³ + 5
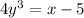
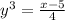
![y=^{\sqrt[3]{(x-5)/(4)}}](https://img.qammunity.org/2018/formulas/mathematics/high-school/c5fe2injilzihwdbujbv2o0acbs7x2o8an.png)
By comparing with given inverse function.
Its clear its the correct option.
C).
Given function: f(x) =
![^{\sqrt[3]{x+3}}-5](https://img.qammunity.org/2018/formulas/mathematics/high-school/v6ddbfrf8m2zsnas1fb5uejle4tcwg271a.png)
To find inverse first put y = f(x) then interchange y & x and solve for y
y = f(x)
x = f(y)
![x=^{\sqrt[3]{y+3}}-5](https://img.qammunity.org/2018/formulas/mathematics/high-school/x5dy1b00juge0n7uc1dd2eriwwha6a31bg.png)
![x+5=^{\sqrt[3]{y+3}}](https://img.qammunity.org/2018/formulas/mathematics/high-school/klvvi3xd38965ofuje4h40q7uqfwzs141p.png)
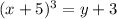

By comparing with given inverse function.
Its clear its not the correct option.
D).
Given function: f(x) = (4x-3)³
To find inverse first put y = f(x) then interchange y & x and solve for y
y = f(x)
x = f(y)
x = (4y-3)³
4y-3 = ∛x
4y = ∛x + 3
![y=\frac{^{\sqrt[3]{x}}+3}{4}](https://img.qammunity.org/2018/formulas/mathematics/high-school/afps80xojoalkjqef1ooaphw9il1su1omy.png)
By comparing with given inverse function.
Its clear its not the correct option.
Therefore, Pair of function Option B is Inverse of Each other.