Question

Number 8 please, What are the coordinates of point C below segment AC that is partitioned at point B in a ratio of 2 to 5.

Answer 1

`\bf \left. \qquad \right.\textit{internal division of a line segment} \\\\\\ A(5,0)\qquad C(x,y)\qquad \qquad 2:5 \\\\\\ \cfrac{AB}{BC} = \cfrac{2}{5}\implies \cfrac{A}{C}=\cfrac{2}{5}\implies 5A=2C\implies 5(5,0)=2(x,y)\\\\ -------------------------------\\\\ { B=\left(\cfrac{\textit{sum of`


`\bf -------------------------------\\\\ B=\left(\cfrac{(5\cdot 5)+(2\cdot x)}{2+5}\quad ,\quad \cfrac{(5\cdot 0)+(2\cdot y)}{2+5}\right)=\boxed{(8,0)} \\\\\\ B=\left( \cfrac{25+2x}{7}~~,~~\cfrac{0+2y}{7} \right)=(8,0)\implies \begin{cases} \cfrac{25+2x}{7}=8\\\\ 25+2x=56\\ 2x=31\\\\ \boxed{x=\cfrac{31}{2}}\\ -------\\ \cfrac{0+2y}{7}=0\\\\ 2y=0\\ \boxed{y=0} \end{cases}`

Answer 2

`((31)/(2),0)`

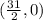
Explanation:

From the given figure it is clear that the coordinates of points are A(5,0) and B(8,0).

Let the coordinates of C are (a,b).

Section formula:

If a point K divides a line segment PQ in m:n and end point of segment are
`P(x_1,y_1)` and
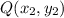`Q(x_2,y_2)`, then the coordinates of point K are

`K=((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n))`

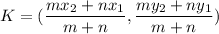
It is given that point B divides the line AC in 2:5.

Using section formula the coordinates of B are

`B=(((2)(a)+(5)(5))/(2+5),((2)(b)+(5)(0))/(2+5))`

`B=((2a+25)/(7),(2b)/(7))`

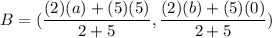
We know that B(8,0).

`(8,0)=((2a+25)/(7),(2b)/(7))`

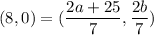
On comparing both sides we get

`8=(2a+25)/(7)`

`56=2a+25`

`56-25=2a`

`31=2a`

`(31)/(2)=a`

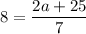
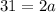
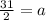
Similarly,

`0=(2b)/(7)\Rightarrow 0=2b\Rightarrow b=0`

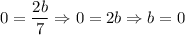
Therefore, the coordinates of C are
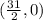`((31)/(2),0)`.