Answer:
1.24 seconds
Step-by-step explanation:
To answer the question we will use the following equation:
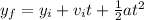
Where:
yf is the final height of the ball, so it is 0m
yi is the initial height of the ball, yi = 20 m
vi is the initial velocity which is vi = -10 m/s because it is downward
a is the acceleration due to gravity a = 9.8 m/s²
t is the time.
So, replacing the values, we get:

To find the time, we need to solve this equation. So, using the quadratic formula, we get:
![\begin{gathered} t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t=\frac{-(-10)\pm\sqrt[]{(-10)^2_{}-4(-4.9)(20)}}{2(-4.9)} \\ t=\frac{10\pm\sqrt[]{100+392}}{-9.8} \\ t=(10\pm22.18)/(-9.8) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/plzi2fsxkr4sj0ydvbqp.png)
Therefore, the values for t are:
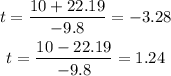
Since t = -3.28 doesn't have sense here, the answer is 1.24 seconds.
The ball reaches the ground after 1.24 seconds.