Question

Suppose we want to choose 5 colors, without replacement, from 8 distinct colors.1. If the order is relevant, how many can be done?2. If it’s not relevant?

Answer 1

(1) From the information given, if we want to choose 5 colors from 8 distinct colors and the order in which the selection is made is relevant, then what we have is a permutation.

The formula is given as;

`nP_r=(n!)/((n-r)!)`

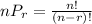
This formula means we need to select/arrange r items out of a total of n items and the anwer derived would be the total number of arrangements possible.

Therefore, we would have;

`\begin{gathered} nP_r\Rightarrow_8P_5 \\ _8P_5=(8!)/((8-5)!)\Rightarrow(8!)/(3!) \\ _8P_5=(8*7*6*\ldots1)/(3*2*1)\Rightarrow(40320)/(6) \\ _8P_5=6720 \end{gathered}`

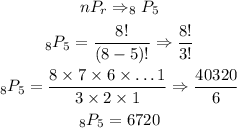
Therefore, if the order is relevant, this selection can be done in 6,720 ways.

(2) If the order is NOT relevant, then what we need to calculate is a combination and the formula is;

`_nC_r=(n!)/((n-r)!r!)`

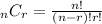
The formula can now be applied as follows;

`\begin{gathered} _nC_r\Rightarrow_8C_5 \\ _8C_5=(8!)/((8-5)!*5!) \\ _8C_5=(8!)/(3!*5!)\Rightarrow(8*7*6*\ldots1)/((3*2*1)*(5*4*\ldots1)) \\ _8C_5=(40320)/(6*120) \\ _8C_5=56 \end{gathered}`

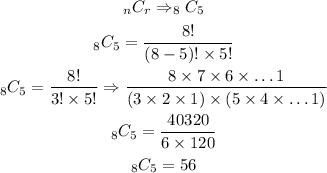
If the order is not relevant, then the selection can be done in 56 ways.