Question

X>-2.5
`√(2x + 5)`what is F'(2)

Answer 1

`f^(\prime)(2)=\frac{1}{\sqrt[]{9}}=(1)/(3)`

Step by step explanation:

To determine the derivate of the following function:

`\begin{gathered} f(x)=\sqrt[]{2x+5} \\ f(x)=(2x+5)^{(1)/(2)} \end{gathered}`

To calculate the derivate of the function, we can use the power rule.

Take the power, 1/2, bring it in front of the parenthesis, and then reduced the power by 1.

`f^(\prime)(x)=(1)/(2)(2x+5)^{-(1)/(2)}`

Then, you have to derivate the intern, which means the parenthesis:

`f^(\prime)(x)=(1)/(2)(2x+5)^{-(1)/(2)}\cdot2`

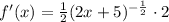
Now, evaluate the derivate in x=2, to find f'(2).

`\begin{gathered} f^(\prime)(x)=\frac{1}{\sqrt[]{2x+5}} \\ f^(\prime)(2)=\frac{1}{\sqrt[]{2(2)+5}} \\ f^(\prime)(2)=\frac{1}{\sqrt[]{9}}=(1)/(3) \end{gathered}`