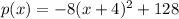Question

The function p(x) = –8x2 – 64x can be written in vertex form p(x) = a(x – h)2 + k, where a =

Answer 1

means compplete the square on one side

basically get into form
`f(x)=a(x-h)^2+k`


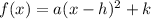
ok, group x terms

`p(x)=(-8x^2-64x)`
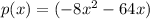
factor out linear coefient (-8)

`p(x)=-8(x^2+8x)`
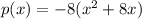
take 1/2 of the linear coefient and square it
8/2=4, 4^2=16
add positive and negaitve of that inside parntheaese

`p(x)=-8(x^2+8x+16-16)`
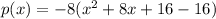
factor perfect square

`p(x)=-8((x+4)^2-16)`
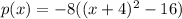
expand

`p(x)=-8(x+4)^2+128`

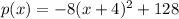
in vertex form it is
`p(x)=-8(x+4)^2+128`