we have

we know that
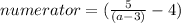
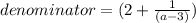
Step

Write the numerator and denominator with a common denominator
Numerator
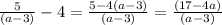
Denominator
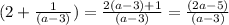
Step
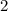
Divide the numerator by the denominator
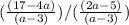
To do this, multiply the numerator by the reciprocal of the denominator.

therefore
the answer is the option
Write the numerator and denominator with a common denominator. Then divide the numerator by the denominator. To do this, multiply the numerator by the reciprocal of the denominator