Question

Etermine whether or not f is a conservative vector field. if it is, find a function f such that f = ∇f. (if the vector field is not conservative, enter dne.) f(x, y) = ex cos(y)i + ex sin(y)j

Answer 1

A vector field
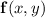
`\mathbf f(x,y)` is conservative *if and only if* we can find a scalar function
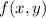
`f(x,y)` for which
`\\abla f=\mathbf f`, which means we're looking for a function
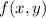
`f(x,y)` such that


`(\partial f)/(\partial x)=e^x\cos y`

`(\partial f)/(\partial y)=e^x\sin y`

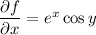
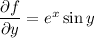
Integrating both sides of the first PDE with respect to
`x`, we get


`f(x,y)=e^x\cos y+g(y)`

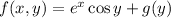
We're assuming the "constant" of integration is some expression independent of
`x`. However, upon differentiating with respect to
`y`, we have


`(\partial f)/(\partial y)=-e^(\sin y)+(\mathrm dg)/(\mathrm dy)=e^x\sin y`

`\implies(\mathrm dg)/(\mathrm dy)=2e^x\sin y`

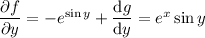
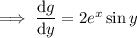
which means
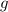
`g` is *not* a function of
`y` alone, contradicting the assumption of the contrary. So our desired
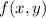
`f(x,y)` does not exist, and therefore
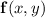
`\mathbf f(x,y)` is *not* conservative.