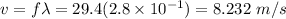Question

A certain transverse wave is described by y(x,t)=bcos[2π(xl−tτ)], where b = 5.90 mm , l = 29.0 cm , and τ = 3.90×10−2 s .

Answer 1

Part A:

The general form of the equation of a transverse wave is given by:


`y(x,t)=A\cos\left[2\pi\left( (x)/(\lambda) - (t)/(T) \right)\right]`

where A is the amplitude,
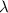
`\lambda` is the wavelength, and T is the period.

Given that a certain transverse wave is described by:


`y(x,t)=bcos[2\pi(xl-t\tau)]`, where b = 5.90 mm , l = 29.0 cm , and \tau = 3.90\times10^{-2} s

Thus, the amplitude is b = 5.90 mm = 5.9\times10^{-3} \ m



Part B:

The general form of the equation of a transverse wave is given by:


`y(x,t)=A\cos\left[2\pi\left( (x)/(\lambda) - (t)/(T) \right)\right]`

where A is the amplitude,
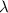
`\lambda` is the wavelength, and T is the period.

Given that a certain transverse wave is described by:


`y(x,t)=bcos[2\pi\left((x)/(l)-(t)/(tau)\right)\right]`, where b = 5.90 mm , l = 29.0 cm , and \tau = 3.90\times10^{-2} s

Thus,


`y(x,t)=bcos[2\pi\left((x)/(l)-(t)/(tau)\right)\right\\ \\ (1)/(\lambda) = (1)/(l) \\ \\ \Rightarrow\lambda= l =28.0 \ cm=\bold{2.8*10^(-1)}`



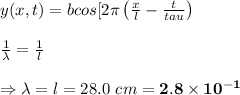
Part C:

The general form of the equation of a transverse wave is given by:


`y(x,t)=A\cos\left[2\pi\left( (x)/(\lambda) - (t)/(T) \right)\right]`

where A is the amplitude,
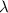`\lambda` is the wavelength, and T is the period.

Given that a certain transverse wave is described by:


`y(x,t)=bcos[2\pi\left((x)/(l)-(t)/(tau)\right)\right]`, where b = 5.90 mm , l = 29.0 cm , and \tau = 3.90\times10^{-2} s

The wave's frequency, f, is given by:


`f= (1)/(T) = (1)/(\tau) = (1)/(3.40*10^(-2)) =\bold{29.4 \ Hz}`



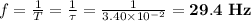
Part D:

Given that the the wavelength is
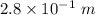`2.8*10^(-1) \ m` and that the wave's frequency is 29.4 Hz

The wave's speed of propagation, v, is given by:


`v=f\lambda=29.4(2.8*10^(-1))=8.232 \ m/s`