Question

The lengths of nails produced in a factory are normally distributed with a mean of 4.634.63 centimeters and a standard deviation of 0.060.06 centimeters. find the two lengths that separate the top 7%7% and the bottom 7%7%. these lengths could serve as limits used to identify which nails should be rejected. round your answer to the nearest hundredth, if necessary.

Answer 1

The prbability that a normally distributed dataset with mean, μ, and standard deviation, σ, is between two values a and b is given by:


`P(a\ \textless \ X\ \textless \ b)=P(X\ \textless \ b)-P(X\ \textless \ a) \\ \\ =P\left(z\ \textless \ (b-\mu)/(\sigma) \right)-P\left(z\ \textless \ (a-\mu)/(\sigma) \right)`

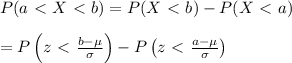
Given that the lengths of nails produced in a factory are normally distributed with a mean of 4.63 centimeters and a standard deviation of 0.06 centimeters.

To find the two lengths that separate the top 7% and the bottom 7%, Let the two required lengths be a and b, because of the symmetry of the normal curve, the probability that the length of a randomly selected nail is between these two lengths is given by:


`P(a\ \textless \ X\ \textless \ b)=1-(0.07+0.07) \\ \\ 2P(X\ \textless \ a)-1=1-0.14 \\ \\ 2P\left(z\ \textless \ (a-4.63)/(0.06) \right)-1=0.86 \\ \\ 2P\left(z\ \textless \ (a-4.63)/(0.06) \right)=1.86 \\ \\ P\left(z\ \textless \ (a-4.63)/(0.06) \right)=0.93=P(z\ \textless \ 1.476) \\ \\ (a-4.63)/(0.06)=1.476 \\ \\ a-4.63=0.06(1.476)=0.08856 \\ \\ a=4.63+0.09=4.72 \ and \ b=4.63-0.09=4.54`

Therefore, the two lengths that separate the top 7% and the bottom 7% are 4.54 and 4.72.