Answer:
Dimensions of the gardens are 6.2 ft by 10.2 ft .
Explanation:
As given
A landscaper wants to create a 12-foot-long diagonal path through a rectangular garden.
The width of the garden is x feet and the length of the garden is 4 more than the width.
Length of the garden = x
Breadth of the garden = x + 4
By using the pythagorean theorem
Hypotenuse² = Perpendicular² + Base²
12² = x² + (x + 4)²
As (a+ b)² = a² + b² + 2ab
As 12² = 144
144 = x² + x² + 16 + 2 × x × 4
144 = 2x² + 16 + 8x
2x² + 8x + 16 - 144 = 0
2x² + 8x - 128 = 0
x² + 4x - 64 = 0
As the general form of the equation is in the form
ax² + bx + c = 0
a = 1 , b = 4 , c = -64
Now by using the discriminant formula
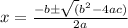
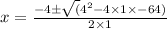
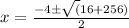
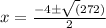
Thus
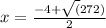
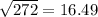
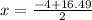
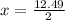
x = 6.2 ft (Approx)
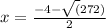
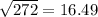
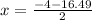
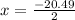
x = -10.2 ft (Approx)
(As the sides of the rectangular garden cannot be negative .)
Thus
x = 6.2 ft
Length of the garden = 6.2 ft
Breadth of the garden = x + 4
= 6.2 + 4
= 10.2 ft
Therefore the dimensions of the gardens are 6.2 ft by 10.2 ft .