Question

Amma send you the screen shot

Answer 1

we have the inequality

`(x)/(3)+\frac{y}{2\text{ }}>1`

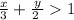
step 1

isolate the variable y

`\begin{gathered} (x)/(3)+\frac{y}{2\text{ }}>1 \\ (y)/(2)>1-(x)/(3) \end{gathered}`

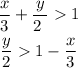
Multiply by 2 both sides

`y\text{ }>2-(2)/(3)x`

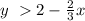
the solution is the shaded area above the dashed line y=2-(2/3)x

so

step 2

Graph the line y=2-(2/3)x

to graph a line we need two points

Find the intercepts of the line

y-intercept (value of y when the value of x is zero)

For x=0

y=2-(2/3)(0) ------> y=2

the y-intercept is (0,2)

x-intercept (value of x when the value of y is zero)

For y=0

0=2-(2/3)x

(2/3)x=2 ----> x=3

x-intercept is (3,0)

step 3

Graph the line

plot the intercepts and join them

step 4

draw the inequality

shaded the area above the dashed line

see the attached figure to better understand the problem'