we have the inequality
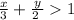
step 1
isolate the variable y
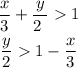
Multiply by 2 both sides
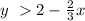
the solution is the shaded area above the dashed line y=2-(2/3)x
so
step 2
Graph the line y=2-(2/3)x
to graph a line we need two points
Find the intercepts of the line
y-intercept (value of y when the value of x is zero)
For x=0
y=2-(2/3)(0) ------> y=2
the y-intercept is (0,2)
x-intercept (value of x when the value of y is zero)
For y=0
0=2-(2/3)x
(2/3)x=2 ----> x=3
x-intercept is (3,0)
step 3
Graph the line
plot the intercepts and join them
step 4
draw the inequality
shaded the area above the dashed line
see the attached figure to better understand the problem'