Since the triangle is not a right triangle, we can use the lay of cosines to find the value of the height. In this case, the height is the side of the triangle labeled as AB. Let c = AB, then, we have the following equation:
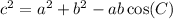
in this case, we have the following information about the triangle:
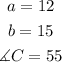
using the law of cosines, we have:
![\begin{gathered} c^2=(12)^2+(15)^2-2(12)(15)\cos (55) \\ =144+225-360\cos (55)=369-206.49=162.51 \\ \Rightarrow c=\sqrt[]{162.51}=12.75 \\ c=12.75\operatorname{cm} \end{gathered}]()
now that we have that the height of the triangle is 12.75cm, we can find the area:
![\begin{gathered} A=(a\cdot c)/(2)=(12\cdot12.75)/(2)=(153)/(2)=76.5 \\ A=76.5\operatorname{cm} \end{gathered}]()
therefore, the area of the triangle is 76.5cm^2