We have to find the standard deviation of this probability distribution.
We have to start by calculating the mean of this distribution.
It can be calculated as:
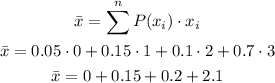
We now can calculate the standard deviation using the last result as:

Answer: the standard deviation is approximately 0.98.