Question

Are the graphs of −5y = 2x + 3 and y=2/4x+4 parallel, perpendicular, or neither?

Answer 1

what we can do is solve both equations for "y", so they end up in slope-intercept form, noticing that the second equation is already in slope-intercept form.

now, keep in mind that parallel lines, have the same slope, and perpendicular ones have a negative reciprocal slope.


`\bf \begin{cases} -5y=2x+3\implies y=\cfrac{2x+3}{-5}\implies &\boxed{y=\stackrel{slope}{-\cfrac{2}{5}}x-\cfrac{3}{5}}\\\\ y=\cfrac{2}{4}x+4\implies &\boxed{y=\stackrel{slope}{\cfrac{1}{2}}x+4} \end{cases}`

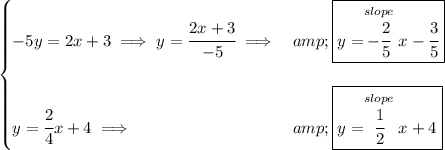
notice, the slopes differ, so clearly they're not parallel.

are they perpendicular? well, the product of the perpendicular ones gives -1, let's check,
`\bf -\cfrac{2}{5}\cdot \cfrac{1}{2}\implies -\cfrac{1}{5}`

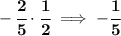
nope, no -1 as product, thus they're not perpendicular either, so they're neither then.