The formula of the distance between 2 points states that the distance AB between points A(a, b) and B(c, d) is found as follows:
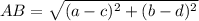
.
Let the points of the polygon be A
(-6,-1), B(-3,-4), C(6,5) and D(3,8). Then, the perimeter of the polygon ABCD is
AB+BC+CD+DA.
We can find each of AB, BC, CD, DA by the Distance Formula as follows:
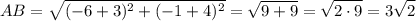 .
.
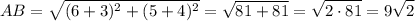 .
.
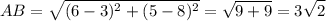 .
.
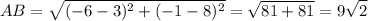 .
.
Thus, the perimeter of the polygon is
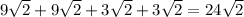 (units).
(units).
Answer:
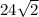 units
units