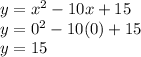Question

Rewrite the equation in vertex form. Name the vertex and y-intercept. y = x^2 – 10x + 15

Answer 1

y = ( x - 5 )²-10

vertex: (5, -10)

y - intercept: ( 0,15)

Explanation:

In order to solve this you first have to create a perfect square trinomial, with the first and second term of the function, which would be X^2 and -10, -10 divided by two would be -5 and -5 squared would be 25, so the equation would be more or less like this:

`y = x^2 – 10x + 15\y = (x^2 – 10x + 15 +10)-10 \\y=(y-5)^2-10\\`

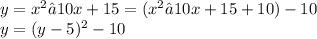
That would be vertex form, and the vertex is calculated by taking the root of the perfect squared trinomial and equalizing it to zero:

x-5=0

x=5 and y= -10 that would be vertex.

And the intersect with the Y-axis is calculated evaluating the equation when x equals 0, that would be:

`y =x^2-10x + 15\\y= 0^2-10(0)+15\\y=15`

Answer 2

y = x² - 10 x + 15 =
= (x² - 10 x + 25) - 25 +15=
= ( x - 5 )² - 10
Answer: y = ( x - 5 )²-10
vertex: (5, -10)
y - intercept: ( 0,15)