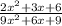Question

1. Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the polynomial in standard form. (1 point)

4, -14, and 5 + 8i


a) f(x) = x4 - 362.5x2 + 1450x - 4984
b) f(x) = x4 - 9x3 + 32x2 - 725x + 4984
c) f(x) = x4 - 67x2 + 1450x - 4984
d) f(x) = x4 - 9x3 - 32x2 + 725x - 4984

2. State how many imaginary and real zeros the function has. (1 point)
f(x) = x5 + 7x4 + 2x3 + 14x2 + x + 7


a) 3 imaginary; 2 real
b) 4 imaginary; 1 real
c) 0 imaginary; 5 real
d) 2 imaginary; 3 real

3. Write a linear factorization of the function.(1 point)
f(x) = x4 + 16x2


a) f(x) = x2 (4x + i)(4x - i)
b) f(x) = x2 (x + 4i)2
c) f(x) = x2 (x + 4i)(x - 4i)
d) f(x) = x2 (4x + i)2

4. Using the given zero, find one other zero of f(x). (1 point)
i is a zero of f(x).= x4 - 2x3 + 38x2 - 2x + 37.


a) -1 + i
b) -i
c) -1 - i
d) 1

5. State the domain of the rational function. (1 point)
f(x) = seven divided by quantity fourteen minus x.


a) All real numbers except 14
b) All real numbers except -14 and 14
c) All real numbers except 7
d) All real numbers except -7 and 7

6. State the vertical asymptote of the rational function.(1 point)
f(x) = quantity x minus seven times quantity x plus four divided by quantity x squared minus four.


a) x = 2, x = -2
b) None
c) x = 7, x = -4
d)x = -7, x = 4

7. State the horizontal asymptote of the rational function. (1 point)
f(x) = quantity x plus nine divided by quantity x squared plus eight x plus five.


a) y = x
b) y = 0
c) y = 9
d) None

8. State the horizontal asymptote of the rational function. (1 point)
f(x) = quantity x squared plus nine x minus nine divided by quantity x minus nine.


a) y = 3
b) None
c) y = 9
d) y = -9

9. Give an example of a rational function that has a horizontal asymptote of y = 2/9.

Answer 1

Question 1:

Given the three zeros

`x = 4`

`x = -14`

`x = 5+8i`
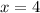
The other zero will be the conjugate pair of
`5+8i`

`x = 5-8i`

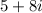
Writing these zeros in factorized form of f(x) gives:

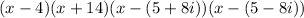
`(x-4)(x+14)(x-(5+8i))(x-(5-8i))` → Multipy out the first two brackets to get

`(x^2+10x-56)(x-5-8i)(x-5+8i)`

`(x^2+10x-56)(x^2-5x+8ix-5x+25-40i-8ix+40i-64i^2)`

`(x^2+10x-56)(x^2-10x+25-64(-1))`

`(x^2+10x-56)(x^2-10x+25+64)`

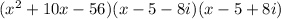
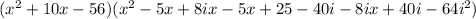
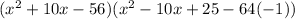
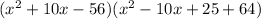
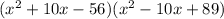
`(x^2+10x-56)(x^2-10x+89)`→ Multiply out further

`x^4-10x^3+89x^2+10x^3-100x^2+890x-56x^2+560x-4984`

`x^4+89x^2-100x^2-56x^2+1450x-4984`

`x^4-67x^2+1450x-4984`

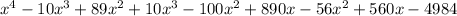
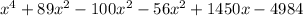
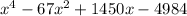
Answer: C
-------------------------------------------------------------------------------------------------------------

Question 2

Given
`x^5+7x^4+2x^3+14x^2+x+7`
Collecting two terms together to get

`(x^5+7x^4)+(2x^3+14x^2)+(x+7)`

`[x^4(x+7)]+[2x^2(x+7)]+[x+7]`
Notice that each group has common factor
`(x+7)`
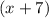
Factorise the common factor gives

`(x+7)[x^4+2x^2+1]`

`(x+7)(x^2+1)(x^2+1)`

The zeros are

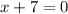
`x+7 = 0` and four of
`x^2+1=0`
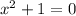
The zero
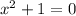
`x^2+1=0` will give an imaginary results

So, f(x) has one real root and four imaginary root

Answer: B
---------------------------------------------------------------------------------------------------------------

Question 3


`f(x) = x^4+16x^2`

`f(x) = x^2(x^2+16)`
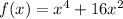
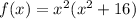
The zeros are

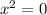
`x^2=0` and
`x^2+16=0`

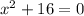
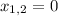
`x_(1,2) = 0` and
`x_(3, 4) = √(-16)`


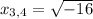
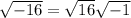
`√(-16)= √(16) √(-1)` which gives two answers:
`4i` and
`-4i`

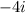
So the factorized form is

`x^2(x+4i)(x-4i)`

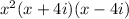
Answer: C
----------------------------------------------------------------------------------------------------------------

Question 4

If
`i` is one of the zeros of
`f(x)` then the other zero would be to conjugate pair of
`i` which is
`-i`

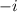
Answer: B
-----------------------------------------------------------------------------------------------------------

Question 5


`f(x) = (7)/(14-x)`
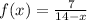
The denominator must not equal zero because we can't divide a quantity by zero (undefined result)
So, we need to find the value of
`x` that would make the denominator equal to zero


`14 - x = 0`

`x = 14`

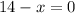
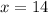
Answer: A
-------------------------------------------------------------------------------------------------------------

Question 6


`f(x) = ((x-7)(x+4))/((x^2-4))`
To find vertical asymptote, set the denominator to zero then find 'x'


`x^2-4=0`

`x^2 = 4`

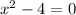
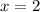
`x = 2` and
`x = -2`

Answer: A
----------------------------------------------------------------------------------------------------------

Question 7


`f(x) = (x+9)/(x^2+8x+5)`
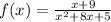
The degree of the denominator is higher than the numerator's, hence the horizontal asymptote is y = 0
------------------------------------------------------------------------------------------------------------

Question 8


`f(x) = (x^2+9x-9)/(x-9)`
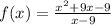
The degree of numerator is higher than the degree of the denominator, hence no horizontal asymptote

------------------------------------------------------------------------------------------------------------

Question 9

To have a horizontal asymptote,
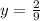
`y = (2)/(9)`, both numerator and denominator must be on the same polynomial degree, and the leading degree have coefficient of 2 and 9

Example:
`(2x^2+3x+6)/(9x^2+6x+9)`