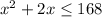Let
x-------> the length of the base of triangle
y-------> the height of the triangle
we know that
the area of the triangle is equal to
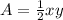
in this problem we have
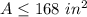
so
 --------> equation
--------> equation

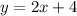 --------> equation
--------> equation
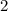
Substitute equation
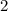 in equation
in equation

![(1)/(2)x[2x+4]\leq 168](https://img.qammunity.org/2018/formulas/mathematics/college/d4c8mr7sqjkjpetqmovfj7sdbv4ynie47s.png)
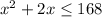
therefore
the answer is
The inequality that can be used to find the possible lengths, x, of the base of the triangle is
![(1)/(2)x[2x+4]\leq 168](https://img.qammunity.org/2018/formulas/mathematics/college/d4c8mr7sqjkjpetqmovfj7sdbv4ynie47s.png) or
or