Question

He accompanying data table describes results from groups of 10 births from 10 different sets of parents. the random variable x represents the number of girls among 10 children. complete the questions below. loading... click the icon to view the data table.

Answer 1

Given the following data table that describes results from groups of 10 births from 10 different sets of parents. The random variable x represents the number of girls among 10 children.


`\begin{tabular} x&p(x)\\[1ex] 0&0.005\\ 1&0.014\\ 2&0.037\\ 3&0.114\\ 4&0.208\\ 5&0.241\\ 6&0.202\\ 7&0.116\\ 8&0.037\\ 9&0.013\\ 10&0.013\\[1ex] &\Sigma p(x)=1 \end{tabular}`

The range rule of thumb says that the range is about four times the standard deviation.

We obtain the standard deviation as follows:

`\begin{tabular} {|c|c|p{2.3cm}|c|c|} x&p(x)&xp(x)&\left(x-E(x)\right)&\left(x-E(x)\right)^2\\[1ex] 0&0.005&0&-5.034&25.341\\ 1&0.014&0.014&-4.034&16.273\\ 2&0.037&0.074&-3.034&9.205\\ 3&0.114&0.342&-2.034&4.137\\ 4&0.208&0.832&-1.034&1.069\\ 5&0.241&1.205&-0.034&0.001\\ 6&0.202&1.212&0.966&0.933\\ 7&0.116&0.812&1.966&3.865\\ 8&0.037&0.296&2.966&8.797\\ 9&0.013&0.117&3.966&15.729\\ 10&0.013&0.13&4.966&24.661\\[1ex] &\Sigma p(x)=1&E(x)=\Sigma xp(x)=5.034 \end{tabular}`

`\begin{tabular} c \left(x-E(x)\right)^2p(x)\\[1ex] 0.127\\0.228\\0.341\\0.472\\0.222\\0.000\\0.188\\0.448\\0.325\\0.204\\0.321\\[1ex]\Sigma\left(x-E(x)\right)^2p(x)=2.876 \end{tabular}`

The standard deviation is given by

`√(\left(x-E(x)\right)^2p(x)) = √(2.876) =1.696`

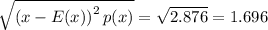
Therefore, the range of values containing the usual numbers of girls in 10 births is given by:

`E(x)\pm2\sigma=5.034\pm2(1.696) \\ \\ =5.034\pm3.392=(5.034-3.392,\ 5.034+3.392) \\ \\ =(1.642,\ 8.426)`

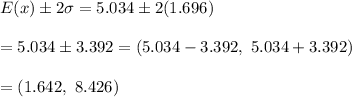
Based on the​ result, 1 girl in 10 births is an unusually low number of​ girls because 1 is not within the normal range of values of number of girls per 10 births.