The image of the point (5, 2) under the same translation is (1, 4).
How to find the coordinates of the image
To find the coordinates of the image of the point (5, 2) under the same translation, use the information given about the translation of the point (2, -8) to (−2, -6).
Let's denote the translation as (a, b).
The translation vector represents the amount by which each coordinate is shifted.
Given that the point (2, -8) translates to (−2, -6), determine the translation vector:
Translation vector =
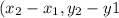 ) = (-2 - 2, -6 - (-8)) = (-4, 2)
) = (-2 - 2, -6 - (-8)) = (-4, 2)
Now, apply the translation vector to the point (5, 2) to find its image:
Image of (5, 2) = (5 + a, 2 + b)
Substitute the values from the translation vector, we have:
Image of (5, 2) = (5 - 4, 2 + 2) = (1, 4)
Therefore, the image of the point (5, 2) under the same translation is (1, 4).