Question

The Pear company sells pPhones. The cost to manufacture x pPhones isC(x) = – 19x^2 + 61000x + 18324 dollars (this includes overhead costs and productioncosts for each pPhone). If the company sells x pPhones for the maximum price they can fetch,the revenue function will be R(x) = - 23x^2 + 149000x dollars.How many pPhones should the Pear company produce and sell to maximimze profit? (Rememberthat profit=revenue-cost.)x=

Answer 1

ou have a revenue function and you have a cost function and you want a profit function.

profit = revenue minus cost, so if you subtract the cost function from the revenue function, you will get the profit function.

your revenue function is y = -23 * x^2 + 149000 * x.

your cost function is y = -19 * x^2 + 61000 * x + 18324.

your profit function will be y = -23 * x^2 + 149000 * x - (-19 * x^2 + 61000 * x + 18324.).

simplify to get y = -23 * x^2 + 149000 * x - 19 * x^2 - 61000 * x - 18324.

combine like terms to get y = -4 * x^2 + 88000 * x - 18324.

that's your profit function.

you want to know when your profit will be maximum.

since this is a quadratic function that's in standard form, you get:

a = -4

b = 88000

c = -18324.

the maximum profit will be when x = -b / 2a.

`x=-(b)/(2a)=(-(88000))/(2(-4))=(88000)/(8)=11000`

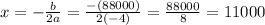
when x = 11000, y =