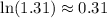Question

I have a difficult Calculus question about linear approximation. Pic Included.

Answer 1

Given the function below

`f(x)=\ln x,\text{ }at\text{ }x=1`

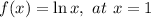
To find the linear approximation, the formula is

`L(x)=f(a)+f^(\prime)(a)(x-a)`

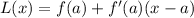
Where

`\begin{gathered} Where,\text{ }a=1 \\ f(1)=\ln1=0 \\ f^(\prime)(x)=(1)/(x) \\ f^(\prime)(1)=(1)/(1)=1 \end{gathered}`

Substitute into the linear approximation formula above

`\begin{gathered} L(x)=f(a)+f^(\prime)(a)(x-a) \\ L(x)=0+1(x-1) \\ L(x)=0+x-1 \\ L(x)=x-1 \end{gathered}`

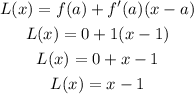
Hence, the linear approximation is

`L(x)=x-1`

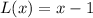
To estimate

`\ln(1.31)`

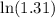
Substitute 1.31 for x into the deduction above,

`\begin{gathered} L(x)=x-1 \\ L(1.31)=1.31-1=0.31 \\ L(1.31)=0.31 \end{gathered}`

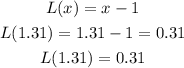
Hence, the answer is

`\ln(1.31)\approx0.31`