Question

How long is the arc intersected by a central angle of pi/2 radians in a circle with a radius of 4.5 cm? Round your answer to the nearest tenth. Use 3.14 for pi

0.3 cm
0.7 cm
2.9 cm
7.1 cm

Answer 1

Answer:-The length of the arc intersected by a central angle
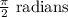`(\pi)/(2)\text{ radians}` is 7.1 cm.

Explanation:-

Let the length of the arc intersected by a central angle be l.

Given:- Central angle
`\theta=(\pi)/(2)\text{ radians}`

Radius r=4.5 cm

We know that ,

`l=\theta\ r\\\Rightarrow\ l=(\pi)/(2)*4.5\\=(3.14*4.5)/(2)=7.065\approx7.1\text{ cm .......[Round to the nearest tenth]}`

Thus, the length of the arc intersected by a central angle
`(\pi)/(2)\text{ radians}` is 7.1 cm.

Answer 2

Central angle = π / 2

length of the arc = angle * radius = (π/2) (4.5 cm)

length of the arc = (3.14 / 2) (4.5) cm = 7.065 cm ≈ 7.1 cm


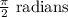Answer: 7.1 cm