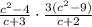Answer:
Option C is correct
the expression which is equivalent to the expression
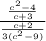 is,
is,
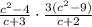
Step-by-step explanation:
Given: The expression is:
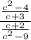
We remember that dividing fraction a by fraction b is the same as multiplying fraction a by the reciprocal of fraction b or vice versa.
Using expression:
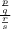
⇒
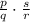
Let p=
 , q=c+3 , r =c+2 and s =
, q=c+3 , r =c+2 and s =
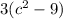
then;
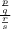 =
=
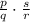
=
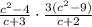
Therefore, the expression which is equivalent to the given expression is,