The binomial distribution is used to calculate the probability of repeated successes if we know the individual odds of success of each event.
The formula is:
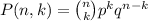
Where n is the number of trials, k is the number of successes, p is the individual success probability, and q = 1 - p.
For n = 20, p = 0.05, it's required to find:
P(x ≤ 3) = P(20, 0) + P(20, 1) + P(20, 2) + P(20, 3)
Applying the formula, for q = 1 - p = 0.95
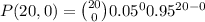
Operating:
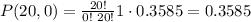
Calculate:
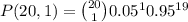
Operate:
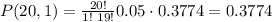
Calculate:
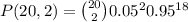
Operate:
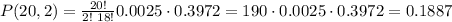
Calculate:
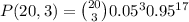
Operate:
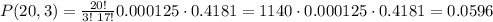
The total probability is:
P(x ≤ 3) = 0.3585 + 0.3774 + 0.1887 + 0.0596 = 0.9842
P(x ≤ 3) = 0.9842