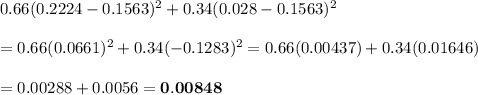Question

What is the variance of a portfolio invested 21 percent each in a and b and 58 percent in c?

Answer 1

Given the following information:


`\begin{tabular} {|p{1.5cm}|p{1.5cm}|p{1.2cm}|p{1.2cm}|p{1.2cm}|} \multicolumn{1}{|p{1.5cm}|}{State of economy}\multicolumn{1}{|p{2.6cm}|}{Probability of State of economy}\multicolumn{3}{|p{4.8cm}|}{Rate of Return if State Occurs}\\[1ex] \multicolumn{1}{|p{1.5cm}|}{}\multicolumn{1}{|p{2.6cm}|}{}\multicolumn{1}c{Stock A}&StockB&Stock C\\[2ex] \multicolumn{1}{|p{1.5cm}|}{Boom}\multicolumn{1}{|p{2.6cm}|}{0.66}\multicolumn{1}{|p{1.27cm}|}{0.09}&0.03&0.34\\ \end{tabular}`

`\begin{tabular} {|p{1.5cm}|p{1.5cm}|p{1.2cm}|p{1.2cm}|p{1.2cm}|} \multicolumn{1}{|p{1.5cm}|}{Bust}\multicolumn{1}{|p{2.6cm}|}{0.34}\multicolumn{1}{|p{1.27cm}|}{0.23}&0.29&-0.14\\ \end{tabular}`

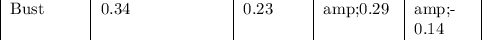
Part A:

The expected return on an equally weighted portfolio of these three stocks is given by:


`0.66[0.33 (0.09) + 0.33 (0.03) + 0.33(0.34)] \\ +0.34[0.33 (0.23) + 0.33(0.29) +0.33(-0.14)] \\ \\ =0.66(0.0297 + 0.0099 + 0.1122)+0.34(0.0759+0.0957-0.0462) \\ \\ =0.66(0.1518)+0.34(0.1254)=0.1002+0.0426=0.1428=\bold{14.28\%}`



Part B:

Value of a portfolio invested 21 percent each in A and B and 58 percent in C is given by

For boom: 0.21(0.09) + 0.21(0.03) + 0.58(0.34) = 0.0189 + 0.0063 + 0.1972 = 0.2224 or 22.24%.

For bust: = 0.21(0.23) + 0.21(0.29) + 0.58(-0.14) = 0.0483 + 0.0609 - 0.0812 = 0.028 or 2.8%

Expected return = 0.66(0.2224) + 0.34(0.028) = 0.1468 + 0.00952 = 0.1563 or 15.63%

The variance is given by


`0.66(0.2224-0.1563)^2+0.34(0.028-0.1563)^2 \\ \\ =0.66(0.0661)^2+0.34(-0.1283)^2=0.66(0.00437)+0.34(0.01646) \\ \\ =0.00288+0.0056=\bold{0.00848}`