Answer: The correct answer would be 112.5 pounds
Step-by-step explanation:
Let us first covert the pound into grams. We know that 1 pound is equal to 453.59 grams.
Thus, 50 pound of fat = 50 x 453.59 = 22,679.5 grams.
We know that, 1 gram of fat releases 9 Kcal of energy. Thus, total energy produced by 22679.5 grams = 9 x 22679.5 = 204,115.5 Kcal
Glycogen is carbohydrate thus, it will produce 4 Kcal of energy per gram.
Thus, 4 x C = 204,115.5 (where C is the grams of glycogen)
⇒ C =

⇒ C = 51,028.875 grams
Using 1 pound = 453.59 grams, we con convert 51,028.875 grams into pounds:
453.59 = 1
1 =
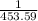
51,028.875 =
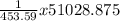
= 112.5 pounds
Thus, 112.5 pound of glycogen would be needed to produce the same amount of energy as produced by 50 pounds of fat.