By using the Pythagorean theorem and the ratio of sides in similar triangles, we found that x = 8/5.
Let’s solve for x in the triangle AED, where <ADE = 90°, ED = 5, AD = 9, and triangle ABC is also a right triangle inside AED with <ABC = 90° and CB = 1.
Steps to solve:
We can use the Pythagorean theorem to find the length of AB in triangle ABC.
Once we have the length of AB, we can use the ratio of the sides of triangle AED to find the length of x.
Solution:
1. Find the length of AB:
Using the Pythagorean theorem in triangle ABC, we get:
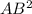 =
=
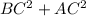
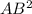 =
=

AB = √(1 +
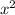 )
)
2. Find the length of x:
From the diagram, we can see that the ratio of AB to AD is equal to the ratio of BC to ED. Therefore, we can write the following equation:
AB/AD = BC/ED
√(1 +
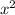 ) / 9 = 1 / 5
) / 9 = 1 / 5
√(1 +
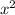 ) = 9/5
) = 9/5
1 +
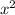 =
=
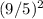
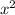 = (9/5)^2 - 1
= (9/5)^2 - 1
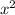 = 64/25
= 64/25
x = √(64/25)
x = 8/5
Therefore, x = 8/5.