Question

A group of students are making a flag to represent their team on game day. The students are going to sew together pieces of fabric to make a design and glue it to the center of the flag. The design is made up of a rectangle, triangle, and semicircle. The dimensions of the design are shown in the diagram.

Answer 1

Step-by-step explanation:

First we have to find the areas of each piece and then add them up.

The area of a triangle is the length of the base multiplied by its height and divided by 2:

`A_{\text{triangle}}=(12in*6in)/(2)=36in^2`

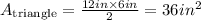
The area of a rectangle is the product of the lengths of the sides:

`A_{\text{rectangle}}=10in*12in=120in^2`

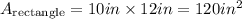
The area of a circle is pi times the radius squared. For a semicircle it's half the area of the circle:

`A_{\text{semicircle}}=(\pi r^2)/(2)=(\pi\cdot5^2)/(2)=(25)/(2)\pi\approx40in^2`

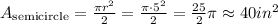
The total area of the flag is:

`\begin{gathered} A=A_{\text{triangle}}+A_{\text{rectangle}}+A_{\text{semicircle}} \\ A=36in^2+120in^2+40in^2 \\ A=196in^2 \end{gathered}`

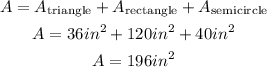
Answer:

B. 196 in²