Question

Write a linear function (y=Mx+b) or exponential function that models the data

Answer 1

We are given a data set and we are asked to write the model that fits the data. We notice that for each step of "x" the values of "y" increase by the same amount. That means that the data follow a linear model, therefore, we will use:

`y=mx+b`

Where:

`\begin{gathered} m=\text{ slope} \\ b=\text{ y-intercept} \end{gathered}`

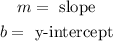
To determine the slope "m" we will use the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where:

`(x_1,y_1),(x_2,y_2)`

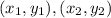
Are data points. From the table we choose the following points:

`\begin{gathered} (x_1,y_1)=(-8,47) \\ (x_2,y_2)=(-7,40) \end{gathered}`

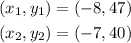
Now, we substitute in the equation for the slope:

`m=(40-47)/(-7-(-8))`

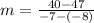
Solving the operations:

`m=(-7)/(-7+8)=-7`

Therefore, the slope is -7. Substituting in the equation of the line we get:

`y=-7x+b`

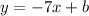
Now, we substitute one of the points to get the value of "b". We will substitute the value x = -8, y = 47, we get:

`47=-7(-8)+b`

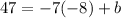
Solving the product:

`47=56+b`

Now we subtract 56 from both sides:

`\begin{gathered} 47-56=56-56+b \\ -9=b \end{gathered}`

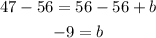
Now, we substitute the value of "b" in the equation of the line:

`y=-7x-9`

And thus we get the line equation.