Question

What is the area of this regular octagon that has been divided into eight congruent triangles?A)90 cm2B)360 cm2C)45 cm2D)180 cm2

Answer 1

The correct answer is option C)
`45cm^2`

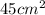
The area of a regular octagon can be divided into 8 congruent isosceles triangles, as you mentioned. To find the area of the octagon, we need to find the area of one of these triangles and multiply it by 8.

Here's how to solve it:

1. Identify the base and height of the triangle: In the image, the base of the triangle is equal to the side length of the octagon, which is 5 cm. The height of the triangle is the apothem of the octagon.

2. Find the apothem: An apothem is the perpendicular line segment drawn from the center of the octagon to the midpoint of a side. In a regular octagon, the apothem can be calculated using the formula: apothem = (square root of 2) * side length / 2.

Plugging in the value of the side length (5 cm), we get: apothem = (square root of 2) * 5 cm / 2 ≈ 3.54 cm.

3. Calculate the area of the triangle: Now that we have the base and height, we can use the formula for the area of a triangle: area = (base * height) / 2.

Substituting the values, we get: area of triangle = (5 cm * 3.54 cm) / 2 ≈ 8.85
`cm^2`.

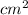4. Find the area of the octagon: Finally, multiply the area of the triangle by 8 to get the total area of the octagon: area of octagon =
`8 * 8.85 cm^2` ≈
`70.8 cm^2`.

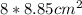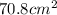Therefore, the closest answer choice to the area of the octagon is C)
`45 cm^2`.

Answer 2

Given:

One octagon is given

Required:

To calculate the area of regular octagon

Step-by-step explanation:

Since we have been divided regular octagon into eight congruent triangles

so firstly we calculate area of triangle with base 5 cm and height 9 cm and then gonna multiply this 8 times to calculate the total area

In the first step we are calculating the area of triangle