Question

A recent poll of 80 randomly selected Californians showed that 38% ( = 0.38) believe they are doing all that they can to conserve water.

The state government would like to know, within a 99% confidence level, the margin of error for this poll. (99% confidence level z*-score of 2.58)

Remember, the margin of error, E, can be determined using the formula E = z*.

To the nearest whole percent, the margin of error for the poll is _____%.

Answer 1

The margin of error given the proportion can be found using the formula


`z* \sqrt{ (p(1-p))/(n) }`

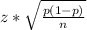
Where

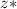
`z*` is the z-score of the confidence level

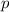
`p` is the sample proportion

`n` is the sample size

We have

`z*=2.58`

`p=0.38`

`n=80`

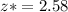
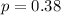
Plugging these values into the formula, we have:

`2.58 \sqrt{ (0.38(1-0.38))/(80) } =0.14`

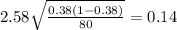
The result 0.14 as percentage is 14%

Margin error is 38% ⁺/₋ 14%

Answer 2

Answer: 14%

Explanation:

Given: Sample size
`n=80`

sample proportion
`p=0.38`

Confidence level
`z=2.58`

We know that Margin error
`M.E.=z\sqrt{(p(1-p))/(n)}`

`\\\Rightarrow\ M.E.=2.58\sqrt{(0.38(1-0.38))/(80)}`

`\\\Rightarrow\ M.E.=2.58\sqrt{(0.2356)/(80)}`

`\\\Rightarrow\ M.E.=2.58√(0.002945)`

`\\\Rightarrow\ M.E.=2.58*0.054`

`\\\Rightarrow\ M.E.=0.14`

Thus, to the nearest whole percent, the margin of error for the poll is 14%