Question

What is the average rate of change of the function f(x)=480(0.3)^x from x = 1 to x = 5?

Enter your answer, as a decimal, in the box.

Do not round your answer.

__________________

Answer 1

average = [f(15) - f(1)] / (5 - 1)
average = [480(0.3)^5 - 480(0.3)^1] / 4
average = [480(0.3)^5 - 480(0.3)^1] / 4
average = (1.1664 - 144)/4
average = -35.7084

Answer 2

Answer: The average rate of change of function f(x) is -35.7084.

Step-by-step explanation:

The given function is,

`f(x)=480(0.3)^x`

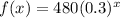
Where to find the rate of change of function from x=1 to x=5.

Put x=1

`f(1)=480(0.3)^(1)=144`

put x=5.

`f(5)=480(0.3)^(5)=1.1664`

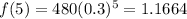
Rate of change is,

`Slope=\frac{\text{Change is f(x)}}{\text{Change is x}}`

`m=(f(5)-f(1))/(5-1)`

`m=(1.1664-144)/(4)`

`m=(-142.8336)/(4)`

`m=-35.7084`

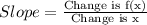
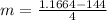
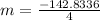
Therefore the rate of change is -35.7084. It means the function f(x) decreases by 35.7084 units as x increases by 1 unit.