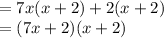Question

1. Multiply.

(7x+3)(4x−5)


2. Factor.

49x^8−16y^14


3. Factor.

7x^2+16x+4

Answer 1

`(a) 28x^2-23x-15`

`(b) (7x^4-4y^(7))(7x^4+4y^(7))`

`(c)(7x+2)(x+2)`

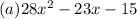
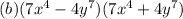
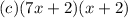
Explanation:

1. (7x+3)(4x−5)

First, Distribute

(7x+3)(4x−5) = 7x(4x-5)+3(4x-5)

Next, we expand the brackets

`7x(4x-5)+3(4x-5)=28x^2-35x+12x-15`

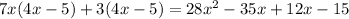
Simplifying like terms

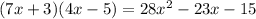
`(7x+3)(4x-5)=28x^2-23x-15`

2.
`49x^8-16y^(14)`

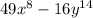
Looking at the terms, you notice that each of the numbers is a perfect square.

`49x^8-16y^(14)=7^(2)x^8-4^2y^(14)`

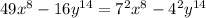
Next, we express the variable terms as a power of 2. This is to enable us apply a particular principle in factorization.

`7^(2)(x^4)^2-4^2(y^(7))^2= (7x^4)^(2)-(4y^(7))^2`

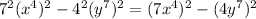
Now, we apply the Principle of Difference of Two Squares.

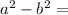`a^2-b^2=`(a-b)(a+b)

Therefore:

`(7x^4)^(2)-(4y^(7))^2=(7x^4-4y^(7))(7x^4+4y^(7))`

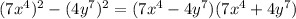
3.
`7x^2+16x+4`

`7x^2+16x+4 = 7x^2+14x+2x+4`

`=7x(x+2)+2(x+2)\\ =(7x+2)(x+2)`

Answer 2

1. (7x+3)(4x−5) =

multiply everything by each other than combine like terms

= 28x^2-23x-15

2. 49x^8−16y^14

rewrite 49x^8 as (7x^4)^2, rewrite -16y^14 as -(4y^7)^2

then factor to get (7x^4 +4y^7)(7x^4 -4y^7)

3. 7x^2+16x+4 = (7x+2)(x+2)