Question

In the diagram, GB = 2x + 3..

What is GB?

A.5 units
B.10 units
C.15 units
D.30 units

Answer 1

Answer: The correct option is (C) 15 units.

Step-by-step explanation: We are given to find the length of GB in the figure.

Given that

FG = 5x and GA = x + 9.

From the figure, we note that DC, EB and FA are the medians of ΔDEF drawn from the vertices D, E and F respectively.

Since, the medians intersect at the point G, so G is the centroid of ΔDEF.

We know that the centroid divides each median of a triangle in the ratio 2 : 1, so we have

`FG:GA=2:1\\\\\\\Rightarrow (FG)/(GA)=(2)/(1)\\\\\\\Rightarrow (5x)/(x+9)=2\\\\\\\Rightarrow 5x=2x+18\\\\\Rightarrow 3x=18\\\\\Rightarrow x=6.`

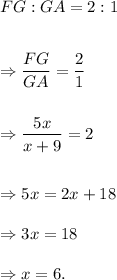
Therefore, the length of GB will be

`GB=2x+3=2*6+3=12+3=15~\textup{units}.`

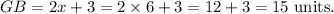
Thus, the length of GB is 15 units.

Option (C) is correct.

Answer 2

`\boxed{\boxed{GB=15\ units}}`

Solution-

From the attachment,

AD = AE, so FA is a median.

BD = BF, so BE is a median.

CF = CE, so DC is a median.

And G is the centroid.

From the properties of centroid, we know that

The centroid divides each median in a ratio of 2:1

So,

`\Rightarrow FG:AG=2:1`

`\Rightarrow (FG)/(AG)=(2)/(1)`

`\Rightarrow FG=2* AG`

`\Rightarrow 5x=2* (x+9)`

`\Rightarrow 5x=2x+18`

`\Rightarrow 3x=18`

`\Rightarrow x=6`

So, GB will be
`2(6)+3=15` units