Question

3. Part A Use addition and your results from questions 1 and 2 to write a polynomial in standard form that represents the area of the entire library. Write an expression for the length of the entire library. Part BExplain why the length and width of the library are factors of the area polynomial.

Answer 1

Part A.

From the given figure, we know that the bookshelf area is

`20x^2+110x+120`

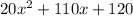
and the area of the entire library is the sum of the bookshelf area plus the reading area. This last area is given by

`A_{\text{reading}}=((x+3)+x+(x+3))^2`

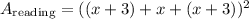
becuase this area has a square shape. By combining similar terms, we can rewritte this area as follows

`A_{\text{reading}}=(3x+6)^2`

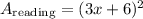
By expanding this result, we get

`A_{\text{reading}}=9x^2+36x+36`

Now ,we will add this area with the bookshelf area in order to get the entire area of the library, that is,

`\begin{gathered} A=A_{\text{bookshelf}}+A_{\text{reading}} \\ A=20x^2+110x+120+9x^2+36x+36 \end{gathered}`

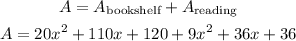
then, by combining similar terms, the area of the entire library is

`A=29x^2+146x+156`

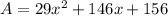
Part B.

Because the area of the entire library has a rectangular shape and its area is given by

`A=\text{width}* length`

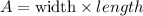
with the width given by

`\text{width}=3x+6`

and length

`\text{length}=3(5+2x)`