Question

What tension would you need to make a middle c (261.6 hz) fundamental mode on a 1 m string (for example, on a harp)? the linear mass density is 0.02 g/cm?

Answer 1

The frequency of middle C on a string is
f = 261.6 Hz.

The given linear density is
ρ = 0.02 g/cm = (0.02 x 10⁻³ kg)/(10⁻² m)
= 0.002 kg/m

The length of the string is L = 1 m.

Let T = the tension in the string (N).
The velocity of the standing wave is

`v= \sqrt{ (T)/(\rho) }`

In the fundamental mode, the wavelength, λ, is equal to the length, L.
That is
Because v = fλ, therefore

`\sqrt{ (T)/(\rho) } =f \lambda = fL \\\\ (T)/(\rho) = (fL)^(2) \\\\ T = \rho (fL)^(2)`

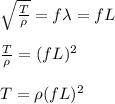
From given information, obtain
T = (0.002 kg/m)*(261.6 1/s)²*(1 m)²
= 136.87 N

Answer: 136.9 N (nearest tenth)