Question

A small shelter for delicate plants is to be constructed of thin plastic material. It will have a square end and a rectangular top and back, with an open bottom and front as shown in the figure. The total are of the four plastic sides is to be 1200in^2.

a) Express the volume of the shelter as a function of the depth x.
b) What dimensions will maximize the volume of the shelter?

Answer 1

Part A

The four plastic sides comprises of two equal squares of area
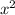
`x^(2)` each and two equal rectangles of area
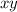
`xy` each.

Given that the total area of the four plastic sides is to be
`1200in^2`, thus:


`2x^2+2xy=1200 \\ \\ \Rightarrow x^2+xy=600 \\ \\ \Rightarrow xy=600-x^2`

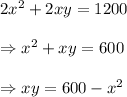
The volume of the figure is given by: Volume = Area of base x depth


`V=(xy)x=x(600-x^2)=600x-x^3`



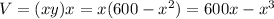
Part B:

For maximum volume, the derivative of V with respect to x will equal 0.


`(dV)/(dx) =0 \\ \\ \Rightarrow600-3x^2=0 \\ \\ \Rightarrow3x^2=600 \\ \\ \Rightarrow x^2=200 \\ \\ \Rightarrow x=\pm √(200) =\pm14.14`

But dimensions has to be positive, thus the value of x which produces maximum volume is x = 14.14

Recall that


`xy=600-x \\ \\ \Rightarrow y= (600)/(x) -x \\ \\ = (600)/(14.14) -14.14 \\ \\ =42.43-14.14 \\ \\ =28.29`

Therefore, the dimensions that will maximize the volume of the shelter is x = 14.14 and y = 28.29