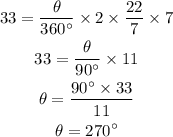Question

How can I find the measure of each angle or arc in a circle

Answer 1

Given:

Find the measure of each angle or arc in a circle.

Step-by-step explanation:

As we know,

The central angle of a circle is 360 degrees.

The central angle that subtends the arc also subtends the same degrees of the arc.

We have the formula to find the measure of angle (or arc) when the arc length (or angle) and radius are given.

The formula is,

`\text{Arc length, }l=(\theta)/(360^(\circ))*2\pi r`

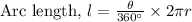
Here, r is the measure of the radius of the circle and θ ( in degrees) is the measure of the angle subtended by the radius.

If θ is measured in radians, then the formula of arc length becomes,

`\text{Arc length, }l=\theta r`

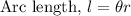
Example:

1. If the radius of the circle is 7 m and the measure of the angle subtended by the radius is 90 degrees, then the arc length is,

`\begin{gathered} l=(90)/(360)*2*(22)/(7)*7 \\ l=11m \end{gathered}`

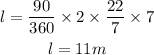
2. If the radius of the circle is 7 m and the measure of the arc length is 33m then the measure of the angle is,

`\begin{gathered} 33=(\theta)/(360^(\circ))*2*(22)/(7)*7 \\ 33=(\theta)/(90^(\circ))*11 \\ \theta=(90^(\circ)*33)/(11) \\ \theta=270^(\circ) \end{gathered}`