Question

Jerrod owes $2,000 on a credit card that charges him an annual percentage rate of 18%. if jerrod stopped making payments, how long would it be before the balance on his credit card reached $4,000?

Answer 1

4 years ( Approx )

Explanation:

Since, the future value of an amount in credit card is,

`A=P(1+(i)/(c))^(t* c)`

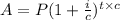
Where, P is the initial amount,

i is the annual rate of interest,

c is the period of compounding,

t is the number of years,

For a credit card, generally we take c = 12 (monthly),

Here, P = $ 2,000,

i = 18 % = 0.18,

Let, the future value of the given amount after t years is $ 4000,

`\implies 2000(1+(0.18)/(12))^(12t)=4000`

`(1+0.015)^(12t)=2`

`1.015^(12t)=2`

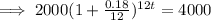
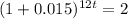
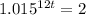
Taking log on both sides,

`12t * log(1.015)=log(2)`

`12t=(log(2))/(log(1.015))\implies t = 3.8796271359\approx 4`

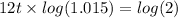
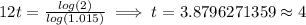
Hence, after approximate 4 years the balance on his credit card reached $4,000.

Answer 2

The Rule of 72 is a basic method to decide how stretched an investment will take to double. It is specified with a fixed annual rate of interest. The annual rate of return would be divided by 72, stockholders can now get an approximate guess of how many years it will take for the original investment to duplicate itself.

So basically, the formula is 72/r where r is the annual rate. So the solution for this is to divide 72 by 18, to get the answer. The answer is 4 years.