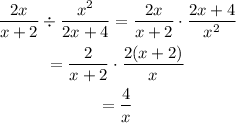Question

Write each of these products and quotients of rational expressions in equivalent form as a single algebraic fraction. Then simplify the result as much as possible.

Answer 1

a. Consider the expression

`(2x+4)/(x^2-6x)\cdot(x^2-36)/(4x+8)`

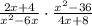
Use the property

`a^2-b^2=(a+b)(a-b)`

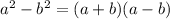
and cancel out the common terms in the numerator and denominator to simplify.

`\begin{gathered} (2x+4)/(x^2-6x)\cdot(x^2-36)/(4x+8)=(2x+4)/(x(x-6))\cdot((x+6)(x-6))/(2(2x+4)) \\ =(x+6)/(2x) \end{gathered}`

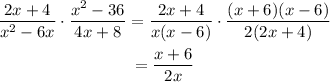
b. Consider the expression

`(x-3)/(7x)\cdot(3x^2)/(x^2-2x-3)`

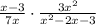
Factorize and cancel out the common terms in the numerator and denominator to simplify.

`\begin{gathered} (x-3)/(7x)\cdot(3x^2)/(x^2-2x-3)=(x-3)/(7)\cdot(3x)/((x-3)(x+1)) \\ =(3x)/(7(x+1)) \end{gathered}`

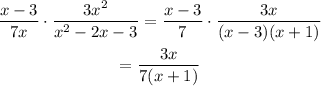
c. Consider the expression

`(x+2)/(x)/(3x+6)/(x^2)`

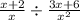
Cross multiply and cancel out the common terms in the numerator and denominator to simplify.

`\begin{gathered} (x+2)/(x)/(3x+6)/(x^2)=(x+2)/(x)\cdot(x^2)/(3x+6) \\ =(x+2)\cdot(x)/(3(x+2)) \\ =(x)/(3) \end{gathered}`

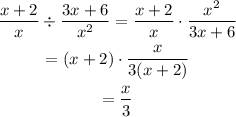
d. Consider the expression

`(2x)/(x+2)/(x^2)/(2x+4)`

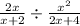
Cross multiply and cancel out the common terms in the numerator and denominator to simplify.

`\begin{gathered} (2x)/(x+2)/(x^2)/(2x+4)=(2x)/(x+2)\cdot(2x+4)/(x^2) \\ =(2)/(x+2)\cdot(2(x+2))/(x) \\ =(4)/(x) \end{gathered}`