Question

Please help! Select the graph for the solution of the open sentence. Click until the correct graph appears.

|x| > 1

(Possible answers attached)


Thanks in advance!

Answer 1

The answer would look like the first picture provided, except it wouldn't be a solid line, it would be dotted line (an > sign or < sign doesn't include the value it's pointing at or away from).

Answer 2

The correct option is 1.

Explanation:

If we have an inequity |x|>a, then the solution set for this inequity is

`x<-a\text{ or }x>a`

`(-\infty,-a)\cup (a,\infty)`

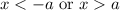
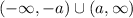
The given inequity is

`|x|>1`

Here a=1, therefore the solution set for this inequality is

`x<-1\text{ or }x>1`

`(-\infty,-1)\cup (1,\infty)`

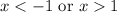
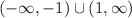
-1 and 1 are not included in the solution set because the sign of inequity are < and >. It means there are open circle at -1 and 1.

Only graph 1 represents the solution set, therefore the correct option is 1.