Question

Which relations are functions? Select EACH correct answer.
Explain how you know.

Answer 1

A relationship between two values can be called a function if every input value produces exactly one output value - in other words, if a function
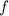
`f` takes in some number
`x` as input, every value of
`x` will produce a single value
`f(x)` as its output. Multiple
`x` values might produce the same
`f(x)`, but no one
`x` value will produce more than one
`f(x)` value.

Here, we can see that the graphs b) and d) capture this kind of relationship, as each value on the
`x` axis is associated with one unique point on the graph. a) interestly enough, can be thought of a function, too; if we describe
`x` as a function of
`y`, then every
`y` value produces exactly one
`x` value. The relationship captured in c) can't be interpreted as a function in either direction, though.

I assume this question is asking for
`y` as a function of
`x` though, in which case options b) and d) will be the correct response.