Question

Consider the equation x2 + 8x = 10.

Get into ax2 + bx+ c form
Find the following:
a=
b=
c=
Show how to solve the equation by using the quadratic formula. Round solutions to the nearest tenth if needed.

Answer 1

1) To write the equation in the standard form
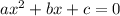
`ax^(2) + bx + c = 0` you need to take everything to the left side and multiply everything, if necessary, to get all whole integers:

`x^(2) + 8x = 10 \\ x^(2) + 8x - 10 = 0`
This will be your standard form of the equation.
2) To find a, b, c you just need to remember that:
- a is a coefficient in front of x^2
- b is a coefficient in front of x
- c is a constant with no x.
So, in your rewritten equation
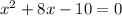
`x^(2) + 8x - 10 = 0` you have a = 1, b = 8, and c = -10
3) To solve the equation using quadratic formula, you need:
- find the Discriminant D, which is
`D = b^(2) - 4ac`
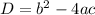
- if D < 0 there is no solution
- if D = 0 there is one solution
`x = - (b)/(2a)`
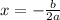
- if D > 0 there are two solutions which are

`x_(1) = (-b + √(D) )/(2a) \\ x_(2) = (-b - √(D) )/(2a)`
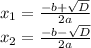
4) Let's solve the equation:
-
`D = b^(2) - 4ac = (8)(8) - (4)(1)(-10) = 64 - (-40) = 104`
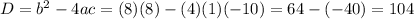
- 104 > 0 => there are 2 solutions
-
`x_(1) = (-b + √(D) )/(2a) = (-(8) + √(104) )/((2)(1)) = (-8 + √(26 * 4) )/(2) = (-8 + 2 √(26) )/(2) = -4 + √(26) \\ x_(2) = (-b - √(D) )/(2a) = (-(8) - √(104) )/((2)(1)) = (-8 - √(26 * 4) )/(2) = (-8 - 2 √(26) )/(2) = -4 - √(26)`
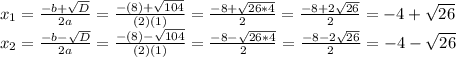
5) So, this is your solution. Good luck!