Given:
• AC = 105.6 meters
,
• m∠BAC = 70.5°
,
• m∠ACB = 38.33°
Let's find the distance between points A and B.
Let's first sketch a triangle representing this situation:
Let's find the length of AB.
To find the length of AB, let's first find the measure of ∠ABC using the triangle angle sum theorem:'
m∠ABC = 180 - 70.5 - 38.833
m∠ABC = 70.667
Now, apply sine rule:
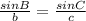
Thus we have:
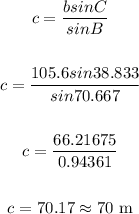
Therefore, the distance between points A and B is 70 meters.
• ANSWER:
D. 70 m