Question

Points A and B are on opposite sides of a lake. A point C is 105.6 meters from A. The measure of ∠BAC is 70.5°, and the measure of ∠ACB is determined to be 38.833°. Find the distance between points A and B (to the nearest meter).A. 49 mB. 23 mC. 35 mD. 70 m

Answer 1

Given:

• AC = 105.6 meters

,

• m∠BAC = 70.5°

,

• m∠ACB = 38.33°

Let's find the distance between points A and B.

Let's first sketch a triangle representing this situation:

Let's find the length of AB.

To find the length of AB, let's first find the measure of ∠ABC using the triangle angle sum theorem:'

m∠ABC = 180 - 70.5 - 38.833

m∠ABC = 70.667

Now, apply sine rule:

`(sinB)/(b)=(sinC)/(c)`

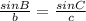
Thus we have:

`\begin{gathered} c=(bsinC)/(sinB) \\ \\ c=(105.6sin38.833)/(sin70.667) \\ \\ c=(66.21675)/(0.94361) \\ \\ c=70.17\approx70\text{ m} \end{gathered}`

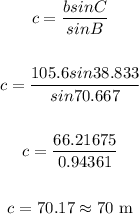
Therefore, the distance between points A and B is 70 meters.

• ANSWER:

D. 70 m