Question

The coordinates of the vertices of ∆PQR are P(-2,5), Q(-1,1), and R(7,3). Determine whether ∆PQR is a right triangle. Show your work and explain your answer!

Answer 1

It is a right triangle. Here is a picture to show why. You can also use the pythagorean theorem. The formula is c= √a^2+b^2. This can also help, to prove that this is a right triangle.

Answer 2

Step 1

Plot the vertices of triangle PQR

`P(-2,5)\ Q(-1,1)\ R(7,3)`

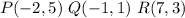
using a graphing tool

see the attached figure

we know that the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

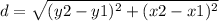
Step 2

Find the distance PR

`P(-2,5)\ R(7,3)`

substitute the values

`d=\sqrt{(3-5)^(2)+(7+2)^(2)}`

`d=\sqrt{(-2)^(2)+(9)^(2)}`

`dPR=√(85)\ units`

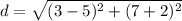
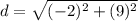
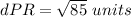
Step 3

Find the distance QP

`Q(-1,1)\ P(-2,5)`

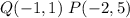
substitute the values

`d=\sqrt{(5-1)^(2)+(-2+1)^(2)}`

`d=\sqrt{(4)^(2)+(-1)^(2)}`

`dQP=√(17)\ units`

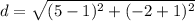
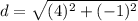
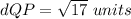
Step 4

Find the distance QR

`Q(-1,1)\ R(7,3)`

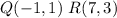
substitute the values

`d=\sqrt{(3-1)^(2)+(7+1)^(2)}`

`d=\sqrt{(2)^(2)+(8)^(2)}`

`dQR=√(68)\ units`

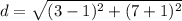
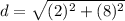
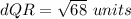
Step 5

If triang;le PQR is a right triangle

then

Applying the Pythagorean Theorem

`PR^(2) =QP^(2) +QR^(2)`

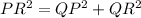
substitute the values

`√(85)^(2) =√(17)^(2) +√(68)^(2)`

`√(85)^(2) =√(17)^(2) +√(68)^(2)`

`85=17+68`

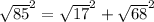
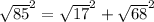
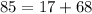
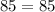`85=85` ---------> is true

therefore

The answer is

The triangle PQR is a right triangle